The Mystery of a Hemisphere

Originally published February 9, 2018 @ 10:32 pm

To make this long (and embarrassing) story short: a friend’s kid had a homework assignment in geometry to calculate the surface area of a conjoined cone, a cylinder, and a hemisphere.

Geometry being the only subject in which I never had anything less than perfect marks, I decided to help out and take a crack at this most basic of problems. And got it wrong. And argued about it. And then summoned my long-abandoned Mathematica programming skills and a dusty laptop that still had the damned thing installed. And the results confirmed my initial solution, and so I argued some more. But I was still wrong.

If you work with computers, you probably know how quickly shell command syntax displaces any real-world knowledge in your brain (unless you’re a Windows admin, in which case you don’t. Sorry about that). The shortest path to a solution, in my estimation, was to break the problem down to its three constituents: the cone, the cylinder, and the hemisphere; calculate the surface area of each separately; add them together; and, finally, subtract the four joining elements – the bases: one for the cone, two for the cylinder, and one for the hemisphere.

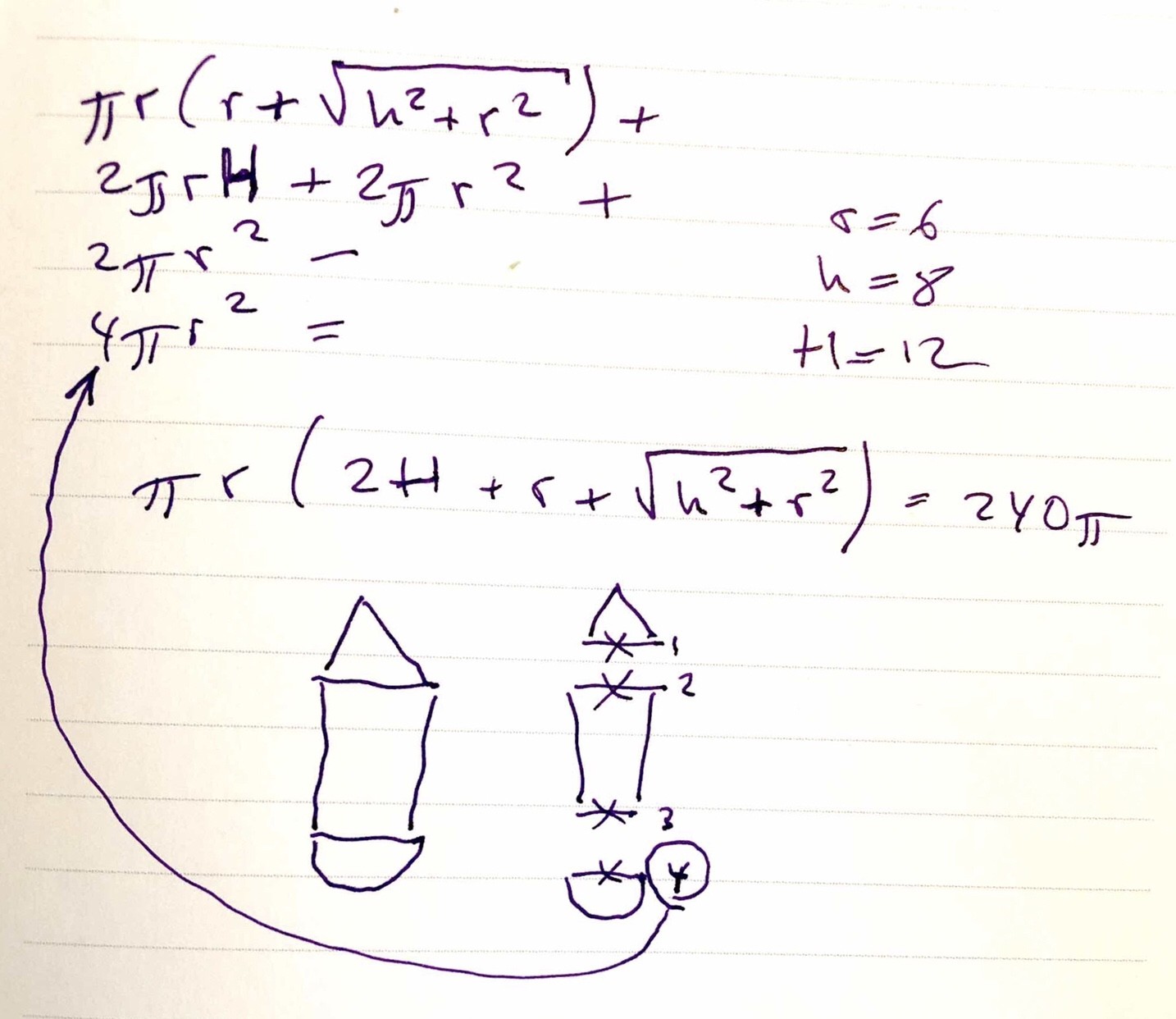
This was a perfectly valid approach. Not the most efficient, but very logical for a “computer guy”. The end result of these uncomplicated calculations turned out to be exactly Pi*r^2 less than the textbook’s answer to the problem. The textbook must be wrong! This happened to me a couple of times and the feeling you get from proving wrong your teacher, the PhDs who authored the textbook, and, indeed, the entire Soviet Ministry of Education (yes, it’s been a while) is best characterized as indescribable joy.

Unfortunately for me, the problem involved the most mysterious and otherworldly shape in all of geometry: the hemisphere. When you calculate the surface area of a cone, a cylinder, and just about any other three-dimensional geometrical shape, the calculations include all of the sides. Of course, they do – it’s surface area – it makes sense! Not so for a hemisphere. Apparently, the base of a hemisphere is surface-area-less. It doesn’t exist. Any geometry textbook will tell you that the surface area of a sphere is 4*Pi*r^2 and, therefore, the surface area of a hemisphere is exactly half that. But doesn’t this make a hemisphere an impossible object in three dimensions? Think about this: it has one side as if it still was a sphere. Like some googly Möbius strip.

If you were to imagine a hollow hemisphere with wall thickness approaching zero, it’s surface area would be approaching that of a complete sphere: 2*Pi*r^2 for the outie and one more of those for the innie. On the other hand, if you think of a hemisphere as half of a perfectly round watermelon (and that’s exactly how one should think about it – a sweet, thirst-quenching, satisfying watermelon), then the surface area would be that of the hemispherical dome and the circular base: 3*Pi*r^2. But, no, it’s 2*Pi*r^2 – the surface area of an impossible three-dimensional object. Why? Because “hemi” means “half” – end of discussion.

This is as if each hypothetical sphere contained a gravitational singularity, such that, when sawed in half, produced a dome-shaped protuberance on one side and on the other – a one-dimensional point of infinite space-time curvature. Thus we have a problem that’s more linguistic than geometrical. And the solution is simple: from now on and until the end of time a hemisphere shall be known as hemiwatermelon to prevent any astrophysics and relativistic mechanics from seeping into the neat and ancient world of geometry. There – problem solved. You’re welcome.